Question

A block of mass 200g is oscillating on the end of a horizontal spring of spring constant 100 N/m and natural length 12 cm. When the spring is stretched to a length of 14 cm, what is the acceleration of the block? [F=ma=kx]

Answer 1

In order to determine the acceleration of the block, use the following formula:

`F=ma`

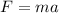
Moreover, remind that for an object attached to a spring the magnitude of the force acting over a mass is given by:

`F=kx`

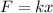
Then, you have:

`ma=kx`

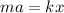
by solving for a, you obtain:

`a=(kx)/(m)`

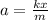
In this case, you have:

k: spring constant = 100N/m

m: mass of the block = 200g = 0.2kg

x: distance related to the equilibrium position = 14cm - 12cm = 2cm = 0.02m

Replace the previous values of the parameters into the expression for a:

Hence, the acceleration of the block is 10 m/s^2