Question

8. Use the point-slope formula to write an equationof a line in slope-intercept form using the points(1/2,5) and (5/2,9)

Answer 1

We have the next two points:

- (1/2,5)

- (5/2,9)

And we must use the point-slope formula to write an equation of a line in slope-intercept

First, we need to calculate the slope of the line using the point-slope formula

`\begin{gathered} y_2-y_1=m(x_2-x_1) \\ m=(y_2-y_1)/(x_2-x_1) \end{gathered}`

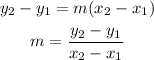
Where (x1, y1) and (x2, y2) are the two points

Now, replacing the points

`m=(9-5)/((5)/(2)-(1)/(2))=(4)/((4)/(2))=(4)/(2)=2`

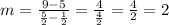
Now, we must replace the slope and one of the two points in the point-slope formula:

`y-y_1=m(x-x_1)`

Replacing m = 2 and (1/2, 5)

`y-5=2(x-(1)/(2))`

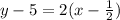
Finally, we must simplify to obtain the slope-intercept form

`\begin{gathered} y-5=2x-1 \\ y=2x-1+5 \\ y=2x+4 \end{gathered}`

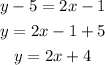
ANSWER:

y = 2x + 4