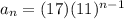Question

17; 187, 2057; 22,627;whats the geometric sequence?

Answer 1

Ok

We have our data:

`17;\text{ 187; 2057; 22627}`

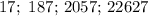
We first find the ratio (r), and that we do dividing one of the values for the inmediatly lower value:

`r=(187)/(17)\Rightarrow r=11`

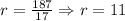
And we doublecheck it by doing the same with other values:

`r=(2057)/(187)\Rightarrow r=11`

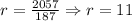
Now that we have the ratio (r), we the add the first term (a):

`a=17`

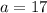
So, by definition the geometric sequence will be going as follows:

`a_n=a\cdot r^(n-1)`

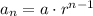
Where a_n will be the geometric sequence, a the first term, r the ratio and n the ammount of terms, so:

`a_n=(17)(11)^(n-1)`

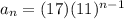
Now if you want to find the 3rd value in the sequence, you just replace n and so on:

`a_3=(17)(11)^(3-1)\Rightarrow a_3=2057`

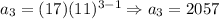
And the fourth:

`a_4=(17)(11)^(4-1)\Rightarrow a_4=22627`

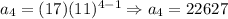
Therefore, the geometric sequence is:

`a_n=(17)(11)^(n-1)`