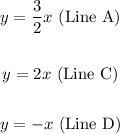• Given the tables of data, you can find the rate of change (the slope of the line) by applying the following formula:
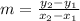
Where the following are two points on the line:
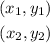
- Table A:
Knowing these points:
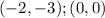
You can substitute the corresponding coordinates into the formula and evaluate:
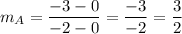
- Table B:
Given the points:
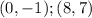
You get:

- Table C:
Having:
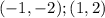
You get that the slope is:
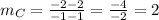
- Table D:
Knowing these two points on the line:
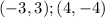
You get the following slope:
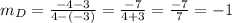
• By definition, the equation of a Proportional Relationship has the following form:

Where the slope "m" is the constant.
That indicates that the value of "y" varies proportionally with the value of "x".
As you can notice, its graph is a line that passes through the Origin.
Therefore, knowing the slope of the Proportional Relationships A, C and D, you can set up the following equations for each one of them:
- For Line A:
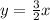
- For Line C:
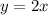
- For Line D:
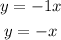
Hence, the answers are:
• Rates of change:
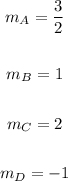
• Function rules for each Proportional Relationship: