Given:
There are given the equation:

Step-by-step explanation:
To find the nature of the root, first, we need to find the value for the discriminant.
So,
From the formula of discriminant:
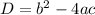
According to the concept:
If,
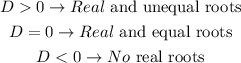
Then,
To find the value of discriminant, put 1 for a, 6 for b, and 9 for c into the above formula:
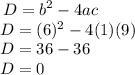
So,
According to the concept, we can say that there are real and equal roots.
Final answer:
hence, the correct option is A.