If we use m compounded per year Bt will be to:
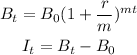
Where:
B0 = deposits = $45900
r = compound yearly interest rate = 1.5% = 0.015
t = years
m = 4
The first quarter's interest
We have following:
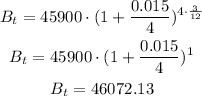
Then:
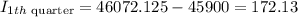
Answer: The interest in first quarter is $172.13
The first quarter's balance
The balance is Bt, therefore:
Answer: The balance after first quarter is $46,072.13