SOLUTION
The angles at points L and O make up a straight line.
These angles are
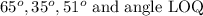
Angles on a straight line = 180 degrees. So
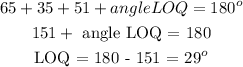
Therefore, angle LOQ = 29 degrees
Angle OPQ at point P is opposite to the angle at point L.
The angle at point L = 65 + 35 = 100 degree
Opposite angle of a parallelogram are equal.
Therefore, angle OPQ = 100 degrees
Angle OPL is alternate to angle PLQ. And angle PLQ = 65 degrees
Alternate angles are always equal.
Therefore, angle OPL = 65 degrees
Before we find LQP, let's find LOP.
Recall that LOQ = 29 degrees. So, LOP = 29 + 51 = 80 degrees
LQP is opposite to LOP. Since opposite angles of a parallelogram are equal,
Therefore, LQP = 80 dgrees.
Angle LPQ is alternate to angle OLP. OLP = 35 degrees
Since alternate angles are equal,
Angle LPQ = 35 degrees