Question

Use the parabola to graph the quadratic function: f(x) = 2x^2+16x+31 Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Answer 1

we have the function

`f(x)=2x^2+16x+31`

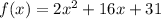
This is a vertical parabola open upward

The vertex is a minimum

Convert the given equation into a vertex form

`f(x)=a(x-h)^2+k`

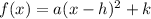
where

(h,k) is the vertex

so

step 1

factor the leading coefficient 2

`\begin{gathered} f(x)=(2x^2+16x)+31 \\ f(x)=2(x^2+8x)+31 \end{gathered}`

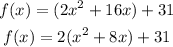
step 2

Complete the square

`\begin{gathered} f(x)=2(x^2+8x+4^2-4^2)+31 \\ f(x)=2(x^2+8x+4^2)+31-32 \\ f(x)=2(x^2+8x+4^2)-1 \end{gathered}`

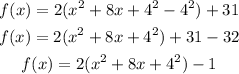
step 3

Rewrite as a perfect square

`f(x)=2(x+4)^2-1`

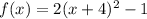
The vertex is the point (-4,-1)

Find out the y-intercept (value of f(x) when the value of x=0)

In the original expression

`\begin{gathered} f(x)=2(0)^2+16(0)+31 \\ f(x)=31 \end{gathered}`

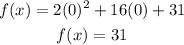
The y-intercept is the point (0,31)

using a graphing tool

Find out another point

For x=-2

substitute

`\begin{gathered} f(x)=2(-2+4)^2-1 \\ f(x)=2(2)^2-1 \\ f(x)=7 \end{gathered}`

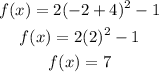
so

the other point is (-2,7)