Question

Find the average rate of change of f(x)xx over the following intervals.

Answer 1

We are given the following function:

`f(x)=x^3-2x+6`

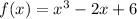
And we are asked to determine the average rate of change between points -8 and -4. To do this we will use the following formula for the average rate of change "R" of a function f(x) between points "a" and "b":

`R=(f(b)-f(a))/(b-a)`

Replacing the points a = -8 and b = -4 in the formula we get:

`R=(f(-4)-f(-8))/(-4-(-8))`

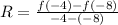
Now we need to determine the value of the function at x = -4. To do this we will replace the value of -4 in the given function:

`f(-4)=(-4)^3-2(-4)+6`

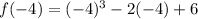
Solving the operations:

`f(-4)=-50`

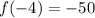
Now we replace the value of x = -8 in the function:

`f(-8)=(-8)^3-2(-8)+6`

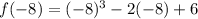
Solving the operations:

`f(-8)=-490`

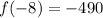
Now we replace the values of the function in the formula for the average rate of change:

`R=(-50-(-490))/(-4-(-8))`

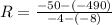
Solving the operations:

`R=(440)/(4)`

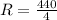
Solving the fraction:

`R=110`

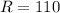
Therefore, the average rate of change is 110.

The same procedure can be used to solve for parts b and c.