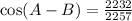Question

Hi! I was absent today in class and missed the whole lesson, can you help me please thank you this is classwork assigment

Answer 1

Given that for positive acute angles A and B:

`\begin{gathered} \cos A=(60)/(61) \\ \\ \tan B=(12)/(35) \end{gathered}`

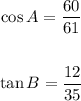
You need to remember that, by definition:

`\begin{gathered} \cos \alpha=(adjacent)/(hypotenuse) \\ \\ \tan \alpha=(opposite)/(adjacent) \end{gathered}`

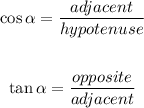
Look at the Right Triangle shown below:

It is also important to remember the following Trigonometric Identity:

`\cos \mleft(A-B\mright)=cosA\cdot cosB+sinA\cdot sinB`

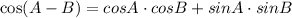
Then, in order to solve this exercise, you need to find:

`\begin{gathered} \cos B \\ \sin A \\ \sin B \end{gathered}`

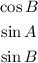
Using the data given in the exercise, you can draw these two Right Triangles (they are not drawn to scale):

Since by definition:

`\sin \alpha=(opposite)/(hypotenuse)`

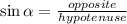
You need to find the opposite side of the first triangle and the hypotenuse of the second triangle. You can do this by applying the Pythagorean Theorem, which states that:

`c^2=a^2+b^2`

Where "c" is the hypotenuse, and "a" and "b" are the legs of the Right Triangle.

Then, the opposite side of the first triangle is:

`\begin{gathered} 61^2=60^2+b^2 \\ \\ 61^2-60^2=b^2 \\ \\ \sqrt[]{61^2-60^2}=b \\ \\ b=11 \end{gathered}`

And the hypotenuse of the second triangle is:

`\begin{gathered} c^2=12^2+35^2 \\ \\ c=\sqrt[]{12^2+35^2} \\ \\ c=37 \end{gathered}`

Now you can determine that:

`\begin{gathered} \cos B=(35)/(37) \\ \\ \sin A=(11)/(61) \\ \\ \sin B=(12)/(37) \end{gathered}`

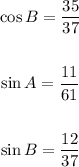
Substitute values into the Trigonometric Identity:

`\begin{gathered} \cos (A-B)=cosA\cdot cosB+sinA\cdot sinB \\ \\ \cos (A-B)=((60)/(61))((35)/(37))+((11)/(61))((12)/(37)) \end{gathered}`

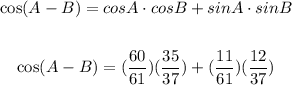
Simplify:

- Multiply the fractions:

`\begin{gathered} \cos (A-B)=(60\cdot35)/(61\cdot37)+(11\cdot12)/(61\cdot37) \\ \\ \cos (A-B)=(2100)/(2257)+(132)/(2257) \end{gathered}`

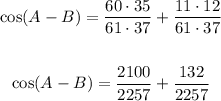
- Add the fractions:

`\begin{gathered} \cos (A-B)=(2100+132)/(2257) \\ \\ \cos (A-B)=(2232)/(2257) \end{gathered}`

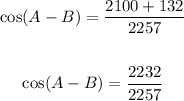
Hence, the answer is:

`\cos (A-B)=(2232)/(2257)`