To find the area of the shaded region, we need to find the area of the hexagon and subtract the area of the circle.
To find the area of the hexagon, we should find the length of the apothem, which is also the radius of the circle.
Since we can divide the hexagon into 6 equilateral triangles, we can use this to find the apothem:
We can take one of those 6 triangles:
The purple line, h is the height of the triangle but also is the apothem of the hexagon. Now, we have two right triangles that we can use to find h (apothem):
And now, we can use the pythagorean theorem to find the length of h:
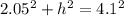
And solve:
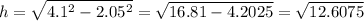
Now. we can find the area of the hexagon and the circle.
The formula for the area of a hexagon is:
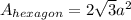
Where a is the apothem. Then:
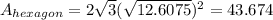
And now, need to calculate the area of the circle:
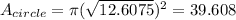
And the area of the shaded region is the difference between the area of the hexagon and the area of the circle:
 The answer, to the nearest tenth, is 4.1 square units
The answer, to the nearest tenth, is 4.1 square units