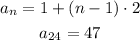
11) Let's firstly examine the sequence:
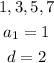
Note that the first term is 1, and this sequence goes increasing by 2 units so the common difference is d=2
2) So we can write an Explicit formula for that Arithmetic Sequence, and then find the 24th term:
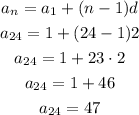
Note that we multiplied the difference by (n-1), in this case, n=24
3) Hence, the 24th term is 47 and the equation is an=1+(n-1)2