6) One of the main characteristics of the logarithmic function is that
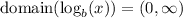
For b>0. Then, in our case, x-2 has to be always greater than zero; thus,
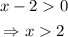
The domain of f(x) is
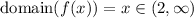
Given the domain, we can calculate the range by evaluating the function in the extremes of the interval
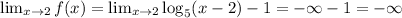
Any function of the form logb(x) ->-infinite when x->0
Similarly,
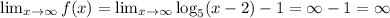
Then, the range of the function is
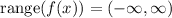
In order to calculate the range of the function, we answer the third part of the question:
As x->infinite, f(x)->infinite
And
As x->2, f(x)->-infinite
To calculate the x-intercept, set f(x)=0 and solve for x, as follows
![\begin{gathered} f(x)=0 \\ \Rightarrow\log _5(x-2)-1=0 \\ \Rightarrow\log _5(x-2)=1 \\ \Leftrightarrow5^1=x-2,\text{ definition of logarithm} \\ \Rightarrow x=7 \end{gathered}]()
The x-intercept is x=7
The only asymptote is when x->2 because, in that case, f(x)->-infinite.
Then, the asymptote is x=2
It's not possible to exactly draw a logarithmic function by hand; however, we can use the information about the asymptote and the x-intercept to be more precise.
The graph of the function is
Table of values of f(x) (3 different values of x)
We already found that f(7)=0, the first value of the table is then
(7,0)
Then,
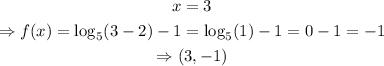
(3,-1)
And
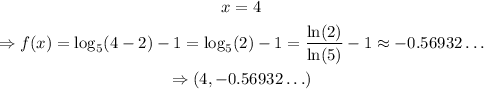
(4, -0.56932...)