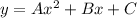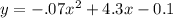To find the power function or the exponential function that models the data, we will use the following standard formula:
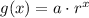
From the table, assuming that g(x) = y, we can solve for the value of a and r.
As we can see from the table, when x = 1, y is 3.5
Substitute it from our equation
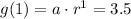
And then, at x = 2, y = 5.7
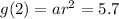
From these 2 equations, let us try to solve for a.
From the first equation, we can rewrite it as
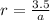
Substitute it to the second equation
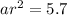
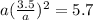
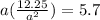
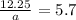
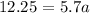
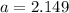
Now, to solve for r, we will just substitute a to the first equation
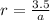
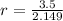
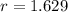
With these, we can now form a formula of:
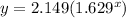
Now, to find the quadratic function the models the data, we will use the standard formula:
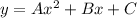
Here, we will use three ordered pairs from the given table
( 1 , 3.5 )
( 2 , 5.7 )
( 3 , 6.5 )
Substitute the first pair to the equation, and solve for A
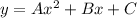
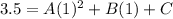
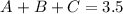
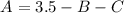
Next, substitute the second pair and the value of A and solve for B
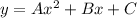
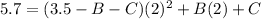

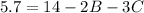
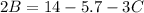
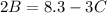
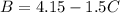
Next, substitute the third pair and the values of A and B to the equation and the solve for C
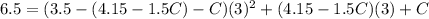

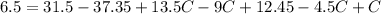
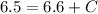
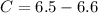
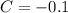
Since B = 4.15 - 1.5C
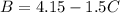

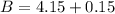
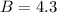
Substitute B and C to solve for A
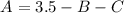
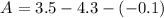
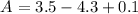
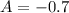
Substitute the values of A, B, and C to the equation