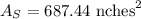To answer that question we can find the surface area of the triangular prism, the surface area of the parallelogram, and after, remove the area where the parallelogram has contact with the triangular prism
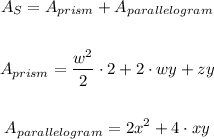
Therefore, we can simplify it to
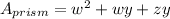
And the parallelogram
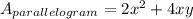
See that one face of the parallelogram has a contact with the prism, it's the area that we must subctract, it's xy, therefore
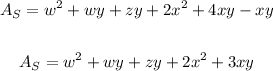
The formula to find the surface area of the figure is
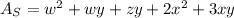
Remember that
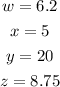
Therefore
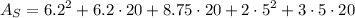
Put it in a calculator