Answer: A.
![\frac{\operatorname{\ln}(1.22)}{5}]()
Step-by-step explanation
We are given the equation:
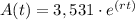
As we are said that the account balance is $4,313 after 5 years, then we can replace the values as follows:
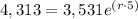
Thus, we have to isolate for r:
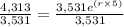
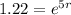
Then, we apply a natural logarithm to both sides of the equation to cancel out the Euler constant.
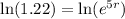
![\operatorname{\ln}(1.22)=5r]()
Finally, we divide both sides of the equation against 5:
