We have a line described with the equation

This describes a horizontal line in the plane, at the height of the x-axis, let's remember that
the horizontal line is the one whose trajectory represents the direction of the horizon as we perceive it. We can also say that the horizontal lines are lines with zero slope.
On the other hand, we must remember that parallel lines are those that, while traveling in the same direction, remain separated at exactly the same distance from each other for exactly the same time.
That is to say that for a line to be parallel we must have another horizontal line.
Now let's determine which equations represent parallel lines one by one.

The above equation represents a slope of zero, i.e. it is a horizontal line so it is a parallel line.

The above equation represents a slope of one, i.e. it is not a horizontal line so it is not a parallel line.
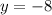
The above equation represents a slope of zero, i.e. it is a horizontal line so it is a parallel line.
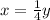
The above equation represents a slope of one, i.e. it is not a horizontal line so it is not a parallel line.
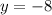
In conclusion, the answer is that y = -2 and y = -8 are parallel lines.