The function is given to be:
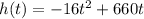
The vertex of the parabola represents the highest (or lowest) point of a parabola. Given the normal form of a quadratic formula:

the vertex is calculated to be:

From the function of the projectile given, we have:
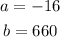
Therefore, the vertex is:
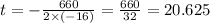
This can be confirmed by graphing the function:
Therefore, the time taken is 20.625 seconds.