Question

14. If the perimeter of a rectangle is 72 feet and the area is at least 288 feet squared find the possible lengths of the rectangle.

Answer 1

Given the perimeter and area of a rectangle you have to determine its possible width and length.

The perimeter of the rectangle can be calculated as:

`\begin{gathered} P=2w+2l \\ 72=2w+2l \end{gathered}`

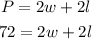
The area of the rectangle can be calculated as:

`\begin{gathered} A=wl \\ 288=wl \end{gathered}`

With this we have determined an equation system:

`\begin{gathered} 72=2w+2l \\ 288=wl \end{gathered}`

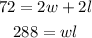
First step: write the first equation in terms of the length:

`\begin{gathered} 72-2w=2l \\ l=(72)/(2)-(2w)/(2) \\ l=36-w \end{gathered}`

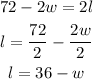
Second step: replace the expression obtained in the second formula:

`\begin{gathered} 288=wl \\ 288=w(36-w) \end{gathered}`

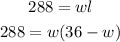
Third step solve the term in parentheses by applying the distributive property of multiplication

`\begin{gathered} 288=36\cdot w-w\cdot w \\ 288=36w-w^2 \end{gathered}`

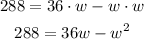
Fourth step, equal to zero and solve using the quadratic formula:

`-w^2+36w-288=0`

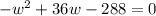
This is a quadratic expression where

a=-1

b=36

c=-288

The quadratic formula is

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Replace with the coefficients to calculate the possible values of the width

`\begin{gathered} w=\frac{-36\pm\sqrt[]{(36)^2-4(-1)(-288)}}{2(-1)} \\ w=\frac{-36\pm\sqrt[]{1296-1152}}{-2} \\ w=\frac{-36\pm\sqrt[]{144}}{-2} \\ w=(-36\pm12)/(-2) \end{gathered}`

Fifth step, calculate both possible values for w:

Positive:

`\begin{gathered} w_1=(-36+12)/(-2) \\ w_1=12ft \end{gathered}`

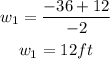
Negative:

`\begin{gathered} w_2=(-36-12)/(-2) \\ w_2=24ft \end{gathered}`

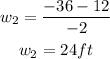
So the possivle values for the width are:

w₁=12ft

w₂=24ft

With this, calculate the possible lengths

Length one:

`\begin{gathered} l_1=36-w_1 \\ l_1=36-12 \\ l_1=24ft \end{gathered}`

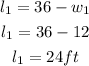
Length two:

`\begin{gathered} l_2=36-w_2 \\ l_2=36-24 \\ l_2=12ft \end{gathered}`

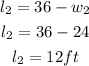
So the possible values of width and length of the rectangle are:

w₁=12ft, l₁=24ft

w₂=24ft, l₂=12ft