Question

I need help solving my geomtry special right triangle problem.

Answer 1

Since the parking lot is a square, all the sides are equal. The diagonal sidewalk forms two equal right triangles, where the diagonal represents the hypotenuse and two sides of the square represents the legs. Using the Pythagorean Theorem we can create an equation for the side of the square.

The Pythagorean Theorem states that the sum of the squaer of the legs is equal to the square of the hypotenuse. If we call the side of the square as x, using this theorem we have the following equation

`x^2+x^2=40^2`

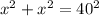
Solving for x, we have

`\begin{gathered} x^2+x^2=40^2 \\ 2x^2=40^2 \\ x^2=(40^2)/(2) \\ x^{}=\sqrt[]{(40^2)/(2)} \\ x^{}=\frac{40^{}}{\sqrt[]{2}} \\ x=20\sqrt[]{2} \end{gathered}`

And this is our value for x.

`x=20\sqrt[]{2}`