Solve the doubts. There might be multiple solutions. There might be no solution

Question

asked Sep 22, 2023 88.4k views

1 Answer

Mouseroot · Answer 1 · 2023-09-27T12:32:45+0000

11) You have the following equation:

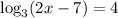
$\log _3(2x-7)=4$

In order to determine if the equation has solution. Proceed as follow:

- Use the equation above as the exponent of 3:

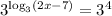
$3^(\log _3(2x-7))=3^4$

- Then, by properties of the logarithms, you can cancel out the log_3:

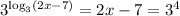
$3^(\log _3(2x-7))=2x-7=3^4$

- Now, consider the second and third member of the previous equation:

And solve for x by adding 7 both sides and then by dividing by 2 both sides:

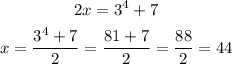
$\begin{gathered} 2x=3^4+7 \\ x=(3^4+7)/(2)=(81+7)/(2)=(88)/(2)=44 \end{gathered}$

Hence, the solution for x = 44