Answer:
• The future value is $635.72
,
• The compound interest is $75.72.
Explanation:
To find the future value at compound interest, we use the formula below:
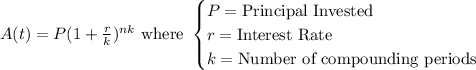
Given:
• Principal, P= $560
,
• Rate, r = 4.25% =0.0425
,
• Period, k = 4 (Quarterly)
,
• Time, n = 3 years
Substitute these values into the formula:
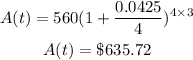
The future value is $635.72
Next, we find the compound interest:
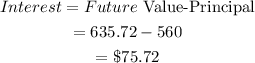
The compound interest is $75.72.