Question

I’m stuck on this one can you help? It’s # 8

Answer 1

Given:

The perpendicular bisector of the sides of triangle RST intersect at point P.

As RC is perpendicular bisector ST, it gives,

`RS=RT\ldots.\ldots\text{.}\mathrm{}By\text{ pependicular bisector theorem}`

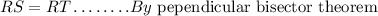
Consider the triangle RPT, PB is perpendicular bisector to RT.

Again by perpendicular bisector theorem,

`\begin{gathered} RP=PT \\ 5x-12=3x+18 \\ 5x-3x=18+12 \\ 2x=30 \\ x=15 \end{gathered}`

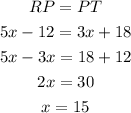
It gives,

`\begin{gathered} RP=5x-12=63 \\ PT=3x+18=63 \end{gathered}`

Using the same aurgument for triangle SPT,

`\begin{gathered} SP=PT \\ SP=63 \end{gathered}`

Answer: SP = 63 inches