Question

Find the length of Jk to the nearest tenth of a foot

Answer 1

We have here a right triangle. We can use trigonometric ratios (sine, cosine, or tangent) to find the length of any side of the triangle.

To do this, we can use angle 77 as a reference angle to find the side JK (the value of x, in this case.)

It is also important the largest side of a right triangle is the hypotenuse (JK).

Having this information, we can proceed as follows:

LJ = 6.9 feet

x = ?

We know that the opposite side to the angle 77 is the side LJ, and knowing this, we can use the sine ratio:

`\sin (77)=(opp)/(hyp)`

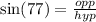
Sine is the opposite side over the hypotenuse, then we have:

`\sin (77)=(6.9ft)/(x)`

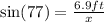
Solving for x, we need to multiply the equation by x to both sides of the equation:

`x\cdot\sin (77)=(6.9ft)/(x)\cdot x\Rightarrow x\cdot\sin (77)=6.9ft\cdot(x)/(x)`

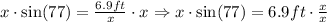
Since x/x = 1. We can now divide both sides of the equation by sin(77):

`x\cdot(\sin(77))/(\sin(77))=(6.9ft)/(\sin(77))\Rightarrow x=(6.9ft)/(\sin (77))`

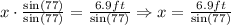
And the value for x (the side JK) is:

`x=(6.9ft)/(0.974370064785)\Rightarrow x=7.08149834377ft`

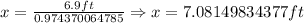
Rounding to the nearest tenth, we have that the value for x, the length of JK = 7.1 feet.