Question

I dotn get this at all step by step explanation please

Answer 1

The speed of the wind is 73.05 km/h and the speed of the plane with no wind is 194.05 km/h.

Explanation:

Let x be the speed of the plane with no wind and y be the speed of the wind.

We must have both speeds in the same unit, so we convert mph to km/h, knowing that 1 mph is equal to 1.609 km/h, so:

`166\text{ mph}\cdot\frac{1.609\text{ km/h}}{1\text{ mph}}=267.1\text{ km/h}`

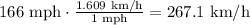
Now, we can establish the following system of equations:

`\begin{gathered} x+y=267.1\rightarrow x=267.1-y \\ \\ x-y=121\rightarrow x=121+y \end{gathered}`

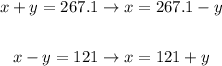
We equate each equation and we are left with the following:

`\begin{gathered} 267.1-y=121+y \\ \\ 2y=267.1-121 \\ \\ y=(146.1)/(2) \\ \\ y=73.05\text{ km/h} \\ \\ \text{ For x:} \\ \\ x=121+73.05 \\ \\ x=194.05\text{ km/h} \end{gathered}`

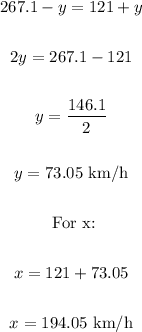
Therefore, the speed of the wind is 73.05 km/h, and the speed of the plane with no wind is 194.05 km/h.