ANSWER:
750 Hz and 692.3 Hz
Explanation:
Given:
f0 = 720 Hz
vs = 14 m/s
vr = 0 m/s
v = 350 m/s
The corresponding formula for the Doppler effect is as follows:
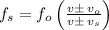
The first scenario the police car is approaching the cafe, therefore:
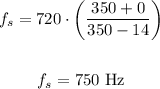
The second scenario the police car is moving away from the cafe, therefore:
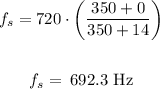
Therefore, the frequency that will be heard when approaching is 750 Hz and when passing the frequency would be 692.3 Hz.