Given:
The total number of face cards is 12.
The total number of cards is 52.
The probability of 2 successive face cards is,
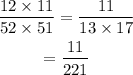
The probability of not getting 2 face cards is,
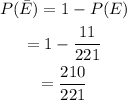
Next, to find the expected value.
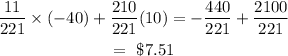
Hence, the expected value of the bet is $7.51.