Question

Given z1 = 12(cos 30° + i sin 30°) and z2 = 4(cos 240° + i sin 240°), what is z1z2?

Answer 1

Suppose we have complex numbers z₁ and z₂ expressed as

`\begin{gathered} z_1=r_1(\cos \theta_1+isin\theta_1) \\ z_2=r_2(\cos \theta_2+isin\theta_2) \end{gathered}`

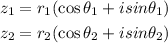
Thus, z₁z₂ is evaluated as

`z_1z_2=r_1r_2(\cos (\theta_1+\theta_2)+i\sin (\theta_1+\theta_2)`

Given the complex numbers z₁ and z₂ as expressed below:

`\begin{gathered} z_1=12_{}(\cos 30\degree+i\sin 30\degree_{}) \\ z_2=4_{}(\cos 240\degree+i\sin 240\degree_{}) \end{gathered}`

Then to evaluate the product of the complex numbers, we have

`\begin{gathered} z_1z_2=r_1r_2(\cos (\theta_1+\theta_2)+i\sin (\theta_1+\theta_2) \\ \text{where} \\ r_1=12 \\ r_2=4 \\ \theta_1=30 \\ \theta_2=240 \\ \text{thus,} \\ z_1z_2=12*4_{}(\cos (30_{}+240_{})+i\sin (30_{}+240)) \\ \Rightarrow48(\cos 270\degree+i\sin 270^{}\degree) \end{gathered}`

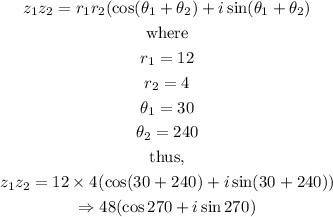
Hence, z₁z₂ is evaluated to be

`48(\cos 270\degree+i\sin 270^{}\degree)`

The first option is the correct answer.