Question

In number 6, determine the value of x in the diagram and what the three angular relationships required to determine x are.

Answer 1

To answer this question we will use the following diagram as reference:

Notice that the angles that measures 80 degrees and a degrees are vertical angles, therefore:

`a^(\circ)=80^(\circ).`

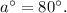
Also, notice that the angles that measures b degrees and (6x+30) degrees are supplementary angles, therefore:

`b^(\circ)+(6x+30)^(\circ)=180^(\circ)\text{.}`

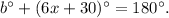
Solving the above equation for b degrees we get:

`\begin{gathered} b^(\circ)+(6x+30)^(\circ)-(6x+30)^(\circ)=180^(\circ)-(6x+30)^(\circ), \\ b^(\circ)=180^(\circ)-(6x+30)^(\circ)\text{.} \end{gathered}`

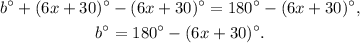
Now, recall that the interior angles of a triangle add up to 180 degrees, therefore:

`50^(\circ)+a^(\circ)+b^(\circ)=180^(\circ)\text{.}`

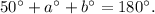
Substituting a degrees and b degrees we get:

`50^(\circ)+80^(\circ)+180^(\circ)-(6x+30)^(\circ)=180^(\circ)\text{.}`

Adding like terms we get:

`310^(\circ)-(6x+30)^(\circ)=180^(\circ).`

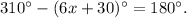
Subtracting 180 degrees we get:

`\begin{gathered} 310^(\circ)-(6x+30)^(\circ)-180^(\circ)=180^(\circ)-180^(\circ), \\ 130^(\circ)-(6x+30)^(\circ)=0^(\circ). \end{gathered}`

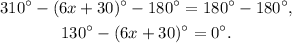
Therefore:

`130-(6x+30)=0.`

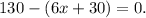
Applying the distributive property we get:

`130-6x-30=0.`

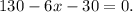
Adding 6x to the above equation we get:

`\begin{gathered} 130-6x-30+6x=0+6x, \\ 100=6x\text{.} \end{gathered}`

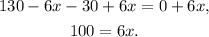
Dividing the above equation by 6 we get:

`\begin{gathered} (100)/(6)=(6x)/(6), \\ x=(50)/(3)\text{.} \end{gathered}`

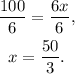
Answer:

(a)

`x=(50)/(3)\text{.}`

(b)

1) Vertical angles.

2) Supplementary angles.

3) The interior angles of a triangle add up to 180 degrees.