Let's put more details in the given figure to understand the problem:
From the figure above, we have three (3) named angles: ∠x, ∠y & ∠z
Using the principle of trigonometric functions, we get:
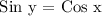
With the given AC = 9 and BC = 12, we can find ∠x using the Tangent Function. We get,
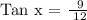
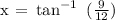
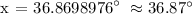
Let's now determine what is Cos x.
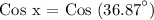
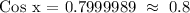
Since Cos x = Sin y, therefore, we can conclude that Sin y = 0.8
ANSWER: Letter B - 0.8