The given problem can be exemplified in the following diagram:
We are given that a ladder is against a wall. According to the diagram, the ladder, the wall, and the floor form a right triangle, therefore, if "T" is the distance from the top to the floor and "B" is the distance from the bottom to the wall we can apply the Pythagorean theorem and we get:

Now, since we want to know the speed, we will derivate implicitly with respect to time on both sides of the equation:
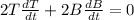
Now we solve for the value of the speed of the top of the ladder, this is dT/dt:
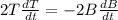
The 2 cancels out:
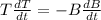
Now we divide both sides by "T":
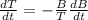
Now, since we determine the value of "T" from the Pythagorean theorem, we get:

Subtracting B squared from both sides:
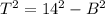
Taking the square root:
![T=\sqrt[]{14^2-B^2}](https://img.qammunity.org/2023/formulas/physics/college/1puvku2h4805shjc4s2u4iibnl0rk7owcq.png)
Now we replace these values in the formula for the velocity:
![(dT)/(dt)=-\frac{B}{\sqrt[]{14^2-B^2}}(dB)/(dt)](https://img.qammunity.org/2023/formulas/physics/college/6gginu4w578qapg7sgm2m4593n6l3rcuk4.png)
Now we have an expression for the velocity of the top of the ladder. Replacing the given values:
![(dT)/(dt)=-\frac{6ft}{\sqrt[]{14^2-(6ft)^2}}(1(ft)/(s))](https://img.qammunity.org/2023/formulas/physics/college/22oikll7w8h225q0s1n8fg1fyy9qnthu9m.png)
Solving the operations we get:

Therefore, the speed of the top of the ladder is -0.47 feet per second.