Question

What The answers of the questions in the attached file please

Answer 1

Given:

A line passes through the points A (1,3) and B (7,1).

The objective is,

a) To find gradient of AB.

b) To find gradient of a line perpendicular to AB.

c) To find the equation line passing throught (4,2) and perpendicular to AB.

Step-by-step explanation:

a)

Consider the given coordinates of line AB as,

`\begin{gathered} (x_1,y_1)=(1,3) \\ (x_2,y_2)=(7,1) \end{gathered}`

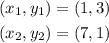
The general formula to find the gradient of line AB is,

`m_(AB)=(y_2-y_1)/(x_2-x_1)`

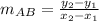
To find gradient of AB:

Substitute the given coordinates in the above gradient formula.

`\begin{gathered} m_(AB)=(1-3)/(7-1) \\ =(-2)/(6) \\ =-3 \end{gathered}`

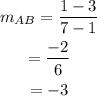
Hence, the gradient of line AB is -3.

b)

To find gradient of perendicular line:

Consider the perpendicular line as CD.

The product of gradients of two perpendicular lines will be -1.

So, the gradient of the perpendicular line CD can be calculated as,

`\begin{gathered} m_(AB)* m_(CD)=-1 \\ m_(CD)=(-1)/(m_(AB)) \\ m_(CD)=-(1)/(-3) \\ m_(CD)=(1)/(3) \end{gathered}`

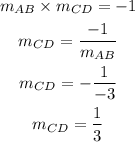
Hence, the gradient of a line perndicular to AB is (1/3).

c)

To find equation of line perpendicular to AB:

Since, the perpendicular line passes through the point,

`(x_1,y_1)=(4,2)`

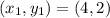
From part (b) the gradient of this perpendicular line is (1/3),

Then, the equation can be calculated using point slope fomula as,

`\begin{gathered} y-y_1=m(x-x_1) \\ y-2=(1)/(3)(x-4) \\ y-2=(x)/(3)-(4)/(3) \\ y=(x)/(3)-(4)/(3)+2 \\ y=(x)/(3)+0.666666\ldots.. \\ y=(x)/(3)+0.67 \end{gathered}`

Hence, the equation of perpendicular line is y = (x/3) + 0.67.

Answers:

a) Gradient AB : (-3)

b) Gradient CD : (1/3)

c) Equation of perpendiular line is y = (x/3) + 0.67.