Question

A guy wire runs from the top of a cell tower to a metal stake in the ground. Jai placesa 8-foot tall pole to support the guy wire. After placing the pole, Jai measures thedistance from the stake to the pole to be 4 ft. He then measures the distance from thepole to the tower to be 33 ft. Find the length of the guy wire, to the nearest foot.

Answer 1

It is easier to solve the exercise if you first draw the situation posed by the statement:

Now, you can find the measure of the cell tower using the following ratio:

`\begin{gathered} \frac{8\text{ ft}}{4\text{ ft}}=\frac{\text{ cell tower}}{37\text{ ft}} \\ \text{ Because the distance from the cell tower to the stake is 33ft + 4ft = 37ft} \\ (8)/(4)=\frac{\text{ cell tower}}{37\text{ ft}} \\ 2=\frac{\text{ cell tower}}{37\text{ ft}} \\ \text{ Multiply by 37 ft from both sides of the equation} \\ 2\cdot37\text{ ft}=\frac{\text{ cell tower}}{37\text{ ft}}\cdot37\text{ ft} \\ 74\text{ ft = cell tower} \end{gathered}`

Finally, since the cell tower, the ground, and the guy wire form a right triangle, then you can use the Pythagorean Theorem to find the length of the guy wire:

`\begin{gathered} a^2+b^2=c^2\text{ }\Rightarrow\text{ Pythagorean Theorem} \\ \text{ Where a and b are the legs and} \\ c\text{ is the hypotenuse} \end{gathered}`

Then, you have

`\begin{gathered} a=37\text{ ft} \\ b=74ft \\ c=\text{?} \end{gathered}`
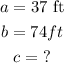
`\begin{gathered} a^2+b^2=c^2 \\ (37\text{ ft})^2+(74\text{ ft})^2=c^2 \\ 1369\text{ ft}^2+5476\text{ ft}^2=c^2 \\ 6845ft^2=c^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{6845ft^2}=\sqrt[]{c^2} \\ 82.7ft=c \\ \text{ Rounding to the nearest foot} \\ 83\text{ ft }=c \end{gathered}`

Therefore, the length of the guy wire is approximately 83 feet.