ANSWER
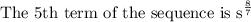
Explanation
Given the sequence below
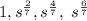
The common ratio of the sequence is given below as
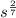
The general formula for finding the nth term of a geometric sequence is
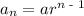
Where,
0. a = first term
,
1. r = common ratio
,
2. n = number of terms
To find the 5th term of the geometric, then n = 5
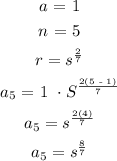
NB: When inputting your answer in the box, use the small letter 's' and not the capital letter S