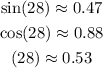Step-by-step explanation
Step 1: We draw the triangle described in the word problem. Since the triangle can be any similar right triangle, we can choose the measure of the sides under the condition that the triangle will be a right triangle and one of its angles measures 28°. For example, the measure of one side can be 5 units.
Step 2: We find the measure of the opposite leg and the hypotenuse.
• Opposite leg: Since it is a right triangle, we can use the trigonometric ratio tan(θ).
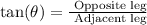
Then, we have:

• Hypotenuse: Since it is a right triangle, we can use the trigonometric ratio cos(θ).
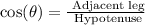
Then, we have:

Step 3: We find the trigonometric ratios sine, cosine and tangent.
• Sine

• Cosine
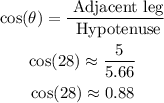
• Tangent

Answer