The given information is the dollars Julia earns varies directly as the number of hours she works.
Also, d=$116.25 when t=15 h.
The formula for the direct variation is:
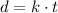
Where k is the constant of variation.
Replace the known values and find k:
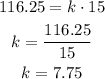
Now, to find t when d=178.25, replace d and k and solve for t in the direct variation equation:
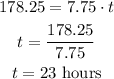
The answer is t=23 hours