Question

The graph of the reciprocal parent function, f(x) = 1/x, is shifted 3 unitsdown and 5 units to the right to create the graph of g(x). What function isg(x)?

Answer 1

Option D is correct.

`g(x)=(1)/(x-5)-3`

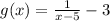
Step-by-step explanation

When a function f(x) is translated horizontally along the x-axis by a units, the new function is represented as

f(x + a) when the translation is by a units to the left.

f(x - a) when the translation is by a units to the right.

When a function f(x) is translated vertically along the y-axis by b units, the new function is represented as

f(x) + b when the translation is by b units upwards.

f(x) - b when the translation is by b units downwards.

For this question,

f(x) = (1/x)

The function is then shifted 3 units down.

f(x) shifted b units down, becomes f(x) - b

So, our question, f(x) shifted 3 units down becomes

f(x) - 3

= (1/x) - 3

Then, there is a further translation of 5 units to the right.

when f(x) is shifted a units to the right, it becomes f(x - a)

So, for our question,

when f(x) is translated 5 units to the right, it becomes f(x - 5)

So, f(x) = (1/x) becomes f(x - 5) = [1/(x - 5)]

So, all together, a translation of 3 units down and 5 units to the right of

f(x) = (1/x) becomes

g(x) = [1/(x - 5)] - 3

Hope this Helps!!!