Question

Can you help with quadratic graph below check if I am going correct

Answer 1

A quadratic function in standard fomr is:

`y=ax^2+bx+c`

a is the number multiplying the quadratic term. b is the number multiplying the x and c is the term without x.

In this case we have:

`f(x)=-x+6-x^2`

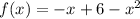
Now if we rearrange as above:

`f(x)=-x^2-x+6`

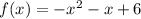
And now we can clearly see that:

a = -1

b = -1

c = 6

now for the table we need to input each term in it. The third row in the x section of the table will be always 6, because is a constant which does not depend of x.

We need to use additional values to the given ones to complete the interval [-4, 3].

We'll use:

-4, -3, -2, -1, -0.5, 0, 1, 2

Now, for -x², the row is:

`\begin{gathered} -(-4)^2=-16 \\ -(-3)^2=-9 \\ -(-2)^2=-4 \\ -(-1)^2=-1 \\ -(-0.5)^2=-0.25 \\ -(0)^2=0 \\ -(1)^2=-1 \\ -(2)^2=-4 \\ -(3)^2=-9 \end{gathered}`

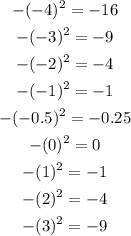
The -x row is:

`\begin{gathered} -(-4)=4 \\ -(-3)=3 \\ -(-2)=2 \\ -(-1)=1 \\ -(-0.5)=0.5 \\ -(0)=0 \\ -(1)=-1 \\ -(2)=-2 \\ -(3)=-3 \end{gathered}`

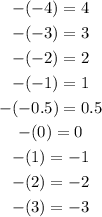
Finally we need to complete the y row. This is the sum of the three values in the x:

The y row is:

`\begin{gathered} -16+4+6=-6 \\ -9+3+6=0 \\ -4+2+6=4 \\ -1+1+6=6 \\ -0.25+0.5+6=6.25 \\ 0+0+6=6 \\ -1-1+6=4 \\ -4-2+6=0 \\ -9-3+6=6 \end{gathered}`

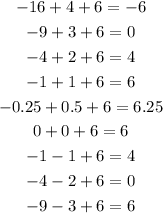
With that, the table is complete, and the problem is solved.