Given:
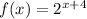
A) Graph the function:
Let us find the intercepts.
When x=0, we get
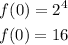
Since it is an exponential function.
So, the graph is,
B) To find the domain:
According to the graph,
The domain is,
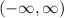
C) To find the range:
According to the graph,
The range is,
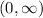
D) To find the asymptote:
The line y=L is a horizontal asymptote of the function y=f(x), if either
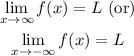
And L is finite.
Here,
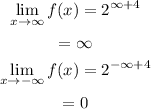
Thus, the horizontal asymptote is y=0.
E) To find the y-intercept:
According to the graph,
When x=0, then f(x)=16.
So,
The y-intercept is 16.