Question

(x-9)(×+4)=168 solve for xI just need reminded how to do the x-9 * x+4 please

Answer 1

The given expression is

`(x-9)(x+4)=168`

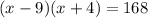
To solve the product, we have to use the distributive property

`x^2+4x-9x-36=168`

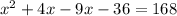
Then, we move all the terms to the left side to combine like terms

`\begin{gathered} x^2+4x-9x-36-168=0 \\ x^2-5x-204=0 \end{gathered}`

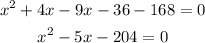
Now, we use the quadratic formula to find the solutions

`x_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Where a = 1, b = -5, and c = -204. Let's replace these values

`\begin{gathered} x_(1,2)=\frac{-(-5)\pm\sqrt[]{(-5)^2-4(1)(-204)}}{2(1)} \\ x_(1,2)=\frac{5\pm\sqrt[]{25+816}}{2}=\frac{5\pm\sqrt[]{841}}{2} \\ x_(1,2)=(5\pm29)/(2) \end{gathered}`

There are two solutions

`\begin{gathered} x_1=(5+29)/(2)=(34)/(2)=17 \\ x_2=(5-29)/(2)=(-24)/(2)=-12 \end{gathered}`

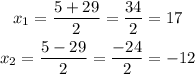
Hence, the solutions are x = 17, and x = -12.