Question

Find the sum of the first three terms of the geometric series represented by the formula.

Answer 1

The easiest way to get the sum is to determine the first three terms using the given formula:

`\text{ A}_n\text{ = }((8)/(25))((5)/(2))^{n\text{ - 1}}`

We get,

First term, n = 1

`\text{ A}_1\text{ = }((8)/(25))((5)/(2))^{n\text{ - 1}}\text{ = }((8)/(25))((5)/(2))^{1\text{ - 1}}\text{ = }((8)/(25))((5)/(2))^0`
`\text{ A}_1\text{ = (}(8)/(25))(1)\text{ = }(8)/(25)`

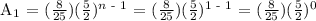
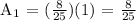
Second term, n = 2

`\text{ A}_2\text{ = }((8)/(25))((5)/(2))^{2\text{ - 1}}\text{ = }((8)/(25))((5)/(2))^1`
`\text{ A}_2\text{ = }((8)/(25))((5)/(2))^{}\text{ = }(40)/(50)\text{ = }(20)/(25)`

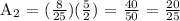
Third term, n = 3

`\text{ A}_3\text{ = }((8)/(25))((5)/(2))^{3\text{ - 1}}\text{ = }((8)/(25))((5)/(2))^2`
`\text{ A}_3\text{ = }((8)/(25))((25)/(4))\text{ = }(200)/(100)\text{ = }(50)/(25)`

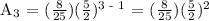
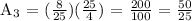
Since the first three terms are already like terms (the same denominator), let's proceed on adding them.

`\text{ Sum = }A_1+A_2+A_3_{}`
`\text{ Sum = }(8)/(25)\text{ + }(20)/(25)\text{ + }(50)/(25)\text{ = }\frac{8\text{ + 20 + 50}}{25}\text{ = }(78)/(25)`

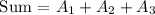
Therefore, the sum of the first three terms is 78/25.