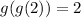Remember the definition for the composition of two functions:
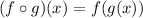
Then, to find each of the compositions, evaluate the "inner" function in the specified value, and then, find the value of the "outer" function evaluated in the result of the inner function.
f(g(3))
Notice that g(3)=4 and f(4)=0. Then:
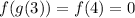
g(f(1))
Notice that f(1)=3 and g(3)=4. Then:
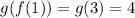
f(f(5))
Notice that f(5)=1 and f(1)=3. Then:
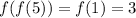
g(g(2))
Notice that g(2)=0 and g(0)=2. Then: