1 Answer

Anubhav C · Answer 1 · 2023-11-21T20:52:31+0000

Notice that the square can be divided into four triangles of height 4cm and base 4cm:

The area of one of the triangles is:

$\begin{gathered} (1)/(2)b\cdot h=(1)/(2)(4\operatorname{cm})(4\operatorname{cm}) \\ =8cm^2 \end{gathered}$

The area of the square is four times the area of one of the triangles:

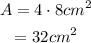
$\begin{gathered} A=4\cdot8cm^2 \\ =32cm^2 \end{gathered}$

Therefore, the area of the square is 32 squared centimeters.

Please log in or register to add a comment.