Question

What are the values of x and z in the solution to the system of linear equations below?

Answer 1

First, we are going to solve for y on the first equation and replace it on the second and third equation as:

`\begin{gathered} -3x-2y+4z=-16 \\ -2y=-16+3x-4z \\ (-2y)/(-2)=(-16+3x-4z)/(-2) \\ y=8-1.5x+2z \end{gathered}`
`\begin{gathered} 10x+10(8-1.5x+2z)-5z=30 \\ 10x+80-15x+20z-5z=30 \\ -5x+15z+80=30 \\ -5x+15z=30-80 \\ -5x+15z=-50 \end{gathered}`
`\begin{gathered} 5x+7y+8z=-21 \\ 5x+7(8-1.5x+2z)+8z=-21 \\ 5x+56-10.5x+14z+8z=-21 \\ -5.5x+22z=-21-56 \\ -5.5x+22z=-77 \end{gathered}`

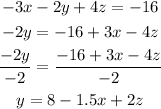
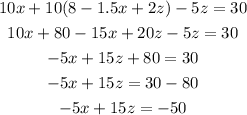
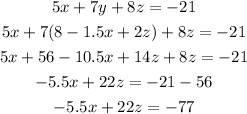
Now, we had 2 equations:

`\begin{gathered} -5x+15z=-50 \\ -5.5x+22z=-77 \end{gathered}`

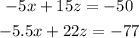
Then, we can solve for x on the first equation an replace it on the second as:

`\begin{gathered} -5x+15z=-50 \\ -5x=-50-15z \\ x=10+3z \end{gathered}`
`\begin{gathered} -5.5x+22z=-77 \\ -5.5(10+3z)+22z=-77 \\ -55-16.5z+22z=-77 \\ 5.5z=-77+55 \\ 5.5z=-22 \\ z=-4 \end{gathered}`

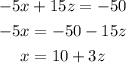
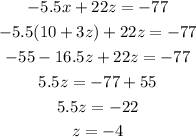
replacing the value of z, we get:

`\begin{gathered} x=10+3z \\ x=10+3\cdot(-4) \\ x=-2 \end{gathered}`

Answer: x=-2 and z=-4