Question

Which quadratic function is represented by the graph?-3O y = 0.5(x + 2)2 + 4o y = 0.5(x + 3)2 - 0.50 y = 0.5(x - 3)2 – 0.5o y = 0.5(x - 2)2 + 4-241(20) 24.0)2(3 -0.5)6x--2

Answer 1

Hello!

First, let's analyze the graph: notice that the concavity is up, so the coefficient a is positive. We also can see that the roots of this graph are 2 and 4.

Other information: the minimum point is (3, -0.5).

Now, let's analyze each alternative:

a. y = 0.5(x+2)² +4

`\begin{gathered} y=0.5\mleft(x+2\mright)^2+4 \\ y=0.5x^2+2x+6 \\ \end{gathered}`

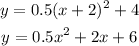
Let's calculate the minimum point of it and compare:

`\begin{gathered} x_V=(-b)/(2\cdot a)=-(2)/(2\cdot0.5)=(-2)/(1)_{}=-2 \\ \\ y_V=-(\Delta)/(4\cdot a)=-(b^2-4\cdot a\cdot c)/(4\cdot a)=-(2^2-4\cdot0.5\cdot6)/(4\cdot0.5)=-(4-12)/(2)=-(-8)/(2)=4 \end{gathered}`

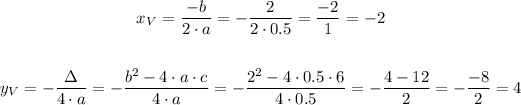
Notice that these coordinates of the minimum point are different as (3, -0.5), so it's false.

b. y = 0.5(x+3)²-0.5

`\begin{gathered} y=0.5\mleft(x+3\mright)^2-0.5 \\ y=0.5x^2+3x+4 \end{gathered}`

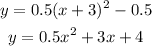
Let's calculate the minimum point too:

`\begin{gathered} x_V=(-b)/(2\cdot a)=(-3)/(2\cdot0.5)=(-3)/(1)=-3 \\ \\ y_V=-(\Delta)/(4\cdot a)=-(b^2-4\cdot a\cdot c)/(4\cdot a)=-(3^2-4\cdot0.5\cdot4)/(4\cdot0.5)=-(9-8)/(2)=-(1)/(2) \end{gathered}`

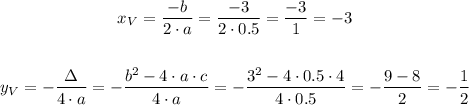
Minimum point: (-3, -0.5) is different as (3, -0.5). False too.

c. y = 0.5(x-3)²-0.5

`\begin{gathered} y=0.5\mleft(x-3\mright)^2-0.5 \\ y=0.5x^2-3x+4 \end{gathered}`

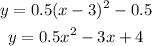
Calculating the minimum point:

`\begin{gathered} x_V=(-b)/(2\cdot a)=-(-3)/(2\cdot0.5)=-(-3)/(1)=3 \\ \\ y_V=-(\Delta)/(4\cdot a)=-(b^2-4\cdot a\cdot c)/(4\cdot a)=-((-3)^2-4\cdot0.5\cdot4)/(4\cdot0.5)=-(9-8)/(2)=-(1)/(2) \end{gathered}`

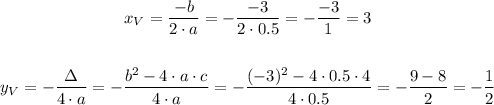
We obtained the point (3, -0.5) as the minimum point and it is equal, so, it's true.

Let me show you all these functions in the cartesian plane to confirm it:

Right answer: Alternative C.