Since the triangle is a right triangle we can draw the triangle like so, calling x the distance corresponding to the base of the triangle and x+5 the height oh the triangle.
now use the formula of the area

we now the area and the corresponding variables for the base and height, replace them on the formula
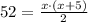
clear for the x

equal the equation to 0 and solve the quadratic equation or by factorization
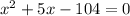
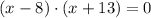
by factorization we know that roots are x=-13 and x=8, since we are talking about a distance the base of the triangle must be 8 ft.
check the answer with the formula of the area

The procedure is correct, the base of the triangle is 8 ft and the height is 13 ft.