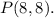Question

Unit 2 ReviewFind point P such that the segment with endpoints A (2, 4) and B (17, 14) in a ratio of 2:3.P:

Answer 1

Let (x,y) and (v,w) two points, if (p,q) divides the segment with end points (x,y) and (v,w) at a ratio a:b we can set the following equalities:

`\begin{gathered} p=(x+v\cdot(a)/(b))/(1+(a)/(b)). \\ q=(y+w\cdot(a)/(b))/(1+(a)/(b)) \end{gathered}`

Substituting the given data we get that:

`\begin{gathered} p=(2+17\cdot(2)/(3))/(1+(2)/(3)), \\ q=(4+14\cdot(2)/(3))/(1+(2)/(3)) \end{gathered}`

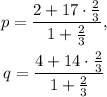
Simplifying the above result we get:

`\begin{gathered} p=(2+(34)/(3))/((5)/(3))=((40)/(3))/((5)/(3))=8, \\ q=(4+(28)/(3))/((5)/(3))=((40)/(3))/((5)/(3))=8. \end{gathered}`

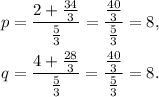
Therefore the coordinates of point P such that the segment with endpoints A (2, 4) and B (17, 14) in a ratio of 2:3 are (8,8).

Answer:

`P(8,8)\text{.}`