Question

Can someone help me with this please? A line segment is divided in two segments, such that the ratio of the long segment to the short segment is equivalent to the golden ratio. If the length of the entire line segment is 7 inches long, what is the length of the longer piece of the divided segment?

Answer 1

From the problem, we have a line segment that is 7 inches long.

It is divided into two segments (long and short) in which the ratio of long segment to the short segment is the golden ratio, Ф = 1.618

Let x = shorter segment

and the longer segment will be (7 - x)

The ratio will be :

`\begin{gathered} \frac{\text{long}}{\text{short}}=\phi \\ \Rightarrow(7-x)/(x)=\phi \\ \Rightarrow(7-x)/(x)=1.618 \end{gathered}`

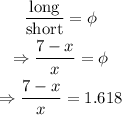
Solve for x :

`\begin{gathered} 7-x=1.618x \\ \text{ Add x to both sides of the equation} \\ 7=1.618x+x \\ 7=2.618x \\ \text{Divide both sides by 2.618} \\ (7)/(2.618)=x \\ x=2.6738 \end{gathered}`

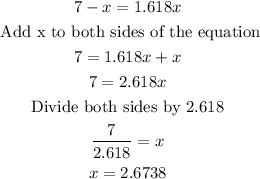
Substitute x = 2.6738 to the equation of long segment :

`\begin{gathered} \text{long}=7-x \\ \Rightarrow7-2.6738 \\ \Rightarrow4.3262 \end{gathered}`

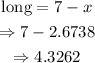
The answer rounded to 2 decimal places is 4.33 inches