Question

Hi I have a question about this scenario that I wrote

Answer 1

79% part.

The binomial distribution formula is given by

`P(x)=C(n,x)p^xq^(n-x)`

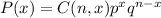
where n is the number of randomly selected, x is the number of successes desired, p is the probability and q = 1-p is the probability of getting a failure.

In our case, p=0.79, q=1-0.79=0.21 and n is 8. Then, the scenario is given by

`P(x)=C(8,x)0.79^x0.21^(8-x)`

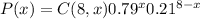
now, we know that x is 6, then we have

`P(6)=C(8,6)0.79^60.21^2`

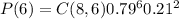
where C(8,6) denote the combination formula:

`C(8,6)=(8!)/((8-6)!6!)=28`

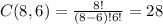
Then, the probability is given by

`\begin{gathered} P(6)=28*0.24*0.0441 \\ P(6)=0.296 \end{gathered}`

that is, the probability that exactly 6 are woman is 0.296