SOLUTION
Given the question in the question tab, the following are the solution steps to answer the question
STEP 1: Write the given equations
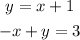
STEP 2: Write the equations in general slope-intercept form
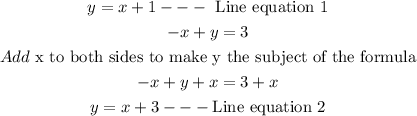
STEP 3: Compare with the general slope-intercept form to get the slopes and the y-intercept

Hence, It can be seen from above that the slopes of the two equations are the same while the y-intercepts are different.
STEP 4: Define infinitely many solutions
An infinitely many solution has both sides equal. For example, 6x + 2=2+6x. If you simplify the equation using an infinite solutions formula or method, you'll get both sides equal, hence, it is an infinite solution. Infinite represents limitless or unboundedness. Infinite solutions would mean that any value for the variable would make the equation true.
From the definition above, it can be seen that there are no infinitely many solutions for the two eqautions.